Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 4

 Un monopolista que puede fi jar el precio o la producción (pero no ambos factores) tal vez desee conocer la demanda de un producto con diversos precios. Tal experimento permite estimar la elasticidad del precio (es decir, la respuesta a variaciones del precio) de la demanda del producto y permite determinar el precio que maximiza las ganancias.

Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 3

 3. Al considerar lo referente a la economía, a un economista quizá le interese estudiar la dependencia del consumo personal respecto del ingreso personal neto disponible (después de impuestos). Con un análisis de este tipo se calcula la propensión marginal a consumir (PMC), es decir, el cambio promedio del consumo ante un cambio, digamos, de un dólar en el ingreso real (ver la figura 1.3).

Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 2

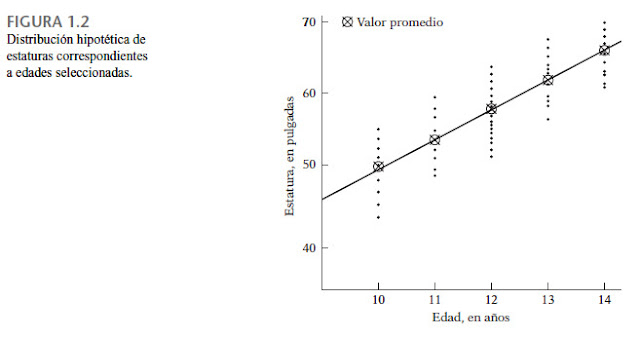
 2. Considere el diagrama de dispersión en la figura 1.2, que presenta la distribución de una población hipotética de estaturas de niños en edades fijas. Observe que existe un rango (distribución) de estaturas correspondiente a cada edad. Es obvia la improbabilidad de que todos los niños de una edad determinada tengan estaturas idénticas. Pero, en promedio, la estatura se incrementa con la edad (por supuesto, hasta cierta edad), que se ve con claridad al trazar una recta (la recta de regresión) por los puntos dentro de los círculos, los cuales representan la estatura promedio de determinadas edades. Por consiguiente, si se conoce la edad, se predice la estatura promedio de dicha edad mediante la recta de regresión.

Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 1

 Considere de nuevo la ley de regresión universal de Galton. A él le interesaba averiguar las razones de la estabilidad en la distribución de estaturas dentro de una población. En el enfoque moderno, la preocupación no es esta explicación, sino averiguar cómo cambia la estatura promedio de los hijos dada la estatura de los padres. En otras palabras, lo que interesa es predecir la estatura promedio de los hijos a partir de la estatura de sus padres. Para ver cómo hacerlo, considere la figura 1.1, que corresponde a un diagrama de dispersión. La fi gura muestra la distribución de las estaturas de los hijos en una población hipotética, correspondiente al conjunto de valores dados o fijos de las estaturas de los padres. Observe que, para cualquier estatura de un padre, existe un rango (distribución) de estaturas de los hijos. Sin embargo, observe también que, a pesar de la variabilidad de la estatura de los hijos conforme al valor de la estatura de los padres, la estatura promedio de los hijos aumenta, por lo general, en la medida en que lo hace la estatura de los padres. Para demostrar esto con claridad, las cruces dentro de los círculos en la figura indican la estatura promedio de los hijos que corresponde a una estatura determinada de los padres. Estos promedios se conectan para obtener la línea recta de la fi gura. Esta línea, como veremos, se conoce como recta de regresión. Dicha recta muestra que el promedio de la estatura de los hijos aumenta conforme crece la de los padres.

Naturaleza del análisis de regresión - Interpretación moderna de la regresión

 La interpretación moderna de la regresión es, sin embargo, muy diferente. En términos generales, se afirma que:

El análisis de regresión trata del estudio de la dependencia de una variable (variable dependiente) respecto de una o más variables (variables explicativas) con el objetivo de estimar o predecir la media o valor promedio poblacional de la primera en términos de los valores conocidos o fi jos (en muestras repetidas) de las segundas.

La importancia trascendental de este enfoque del análisis de regresión se verá claramente sobre la marcha, pero algunos ejemplos sencillos aclararán este concepto básico.

Naturaleza del análisis de regresión - Origen histórico del término regresión

 Francis Galton acuñó el término regresión. En un famoso ensayo, Galton planteó que, a pesar de la tendencia de los padres de estatura alta a procrear hijos altos y los padres de estatura baja, hijos bajos, la estatura promedio de los niños de padres de una estatura determinada tendía a desplazarse, o “regresar”, a la estatura promedio de la población total.1 En otras palabras, la estatura de los hijos de padres inusualmente altos o inusualmente bajos tiende a dirigirse a la estatura promedio de la población. La ley de regresión universal de Galton fue confi rmada por su amigo Karl Pearson, quien reunió más de mil registros de estaturas de miembros de grupos familiares. Pearson descubrió que la estatura promedio de los hijos de un grupo de padres de estatura alta era menor que la estatura de sus padres, y que la estatura promedio de los hijos de un grupo de padres de estatura baja era mayor que la estatura de sus padres; es decir, se trata de un fenómeno mediante el cual los hijos altos e hijos bajos “regresan” por igual a la estatura promedio de todos los demás. En palabras de Galton, se trata de una “regresión a la mediocridad”.

Naturaleza del análisis de regresión

 Como se mencionó en la introducción, la regresión es una herramienta fundamental de la econometría; en este capítulo se considera muy brevemente la naturaleza de este instrumento.

Modelos de regresión uniecuacionales

 En la parte 1 de este texto se presentan los modelos de regresión uniecuacionales. En estos modelos se expresa una variable, llamada dependiente, como función lineal de una o más variables, llamadas explicativas. En modelos de este tipo se supone que si existen relaciones causales entre las variables dependientes y las explicativas, éstas van en una sola dirección: de las variables explicativas a la variable dependiente.

En el capítulo 1 se hace una exposición relacionada con la interpretación, tanto histórica como moderna, del término regresión y se ilustran las diferencias entre las dos interpretaciones con diversos ejemplos tomados de la economía y de otros campos.

En el capítulo 2 se presentan algunos conceptos fundamentales del análisis de regresión con ayuda del modelo de regresión lineal con dos variables, en el cual la variable dependiente se expresa como función lineal de una sola variable explicativa.

En el capítulo 3 continúa el manejo del modelo con dos variables y se introduce lo que se conoce como el modelo clásico de regresión lineal, que tiene diversos supuestos simplifi cadores. Con estos supuestos se presenta el método de mínimos cuadrados ordinarios (MCO) para estimar los parámetros del modelo de regresión con dos variables. La aplicación del método de MCO es sencilla y tiene algunas propiedades estadísticas muy convenientes.

En el capítulo 4 se introduce el modelo clásico de regresión lineal normal (de dos variables), modelo que supone que la variable aleatoria dependiente sigue una distribución de probabilidad normal. Con este supuesto los estimadores MCO obtenidos en el capítulo 3 adquieren algunas propiedades estadísticas más sólidas que las de los modelos clásicos de regresión lineal no normales. Estas propiedades permiten la inferencia estadística y, en particular, las pruebas de hipótesis.

El capítulo 5 se dedica a las pruebas de hipótesis, y se pretende averiguar si los coefi cientes de regresión estimados son compatibles con los valores hipotéticos de tales coefi cientes, valores hipotéticos sugeridos por la teoría y/o por el trabajo empírico previo.

En el capítulo 6 se consideran algunas extensiones del modelo de regresión con dos variables. En particular, se analizan temas como: 1) regresión a través del origen, 2) escalas y unidades de medición, y 3) formas funcionales de modelos de regresión, como doblelogarítmicos, semilogarítmicos y recíprocos.

En el capítulo 7 se considera el modelo de regresión múltiple, en el cual hay más de una variable explicativa, y se muestra cómo se extiende el método MCO para estimar los parámetros de tales modelos. 

En el capítulo 8 se amplían los conceptos del capítulo 5 al modelo de regresión múltiple y se señalan algunas complicaciones propias de diversas variables explicativas.

El capítulo 9, que trata sobre variables explicativas dicótomas o cualitativas, concluye la primera parte del texto. Este capítulo destaca que no todas las variables explicativas necesitan ser cuantitativas (por ejemplo, en escala de razón). Variables como género, raza, religión, nacionalidad y lugar de residencia no son cuantifi cables de manera directa, si bien desempeñan un valioso papel en la explicación de muchos fenómenos económicos.

Metodología de la econometría - Lecturas sugeridas

 El tema de la metodología econométrica es vasto y controvertido. Para los interesados en este tema, sugiero los siguientes libros:

Neil de Marchi y Christopher Gilbert, eds., History and Methodology of Econometrics, Oxford University Press, Nueva York, 1989. En esta colección de lecturas se analizan los primeros trabajos sobre metodología econométrica. El análisis se extiende al método británico de la econometría relacionado con cifras de series de tiempo, es decir, datos recopilados a través de un periodo determinado.

Wojciech W. Charemza y Derek F. Deadman, New Directions in Econometric Practice: General to Specifi c Modelling, Cointegration and Vector Autoregression, Edward Elgar, Hants, Inglaterra, 1997. Los autores critican el método tradicional de la econometría y dan una exposición detallada de nuevos enfoques a la metodología econométrica.

Adrian C. Darnell y J. Lynne Evans, The Limits of Econometrics, Edward Elgar, Hants, Inglaterra, 1990. Este libro presenta un análisis, en cierta medida equilibrado, de los diversos enfoques metodológicos a la econometría, con una renovada fi delidad a la metodología econométrica tradicional.

Mary S. Morgan, The History of Econometric Ideas, Cambridge University Press, Nueva York, 1990. La autora proporciona una perspectiva histórica excelente sobre la teoría y la práctica de la econometría, con un análisis a fondo de las primeras contribuciones de Haavelmo (Premio Nobel de Economía 1990) a la econometría. Con el mismo espíritu, David F. Hendry y Mary S. Morgan antologaron escritos seminales para la econometría en The Foundation of Econometric Analisis, Cambridge University Press, Gran Bretaña, 1995, con el objeto de mostrar la evolución de las ideas econométricas a través del tiempo.

David Colander y Reuven Brenner, eds., Educating Economists, University of Michigan Press, Ann Arbor, Michigan, 1992. El texto presenta un punto de vista crítico, en ocasiones agnóstico, de la enseñanza y práctica de la economía.

Para consultar sobre los temas de estadística y econometría bayesianas, los siguientes libros pueden ser útiles: John H. Dey, Data in Doubt, Basil Blackwell, Oxford, University Press, Inglaterra, 1985; Peter M. Lee, Bayesian Statistics: An Introduction, Oxford University Press, Inglaterra, 1989; y Dale J. Porier, Intermediate Statistics and Econometrics: A Comparative Approach, MIT Press, Cambridge, Massachusetts, 1995. Una referencia avanzada es Arnold Zellner, An Introduction to Bayesian Inference in Econometrics, John Wiley & Sons, Nueva York, 1971. Otro libro de consulta avanzada es Palgrave Handbook of Econometrics. Volumen I. Econometric Theory, Terence C. Mills y Kerry Patterson, eds., Palgrave Macmillan, Nueva York, 2007.

Metodología de la econometría - La función de la computadora

 El análisis de regresión, herramienta de uso diario de la econometría, no sería posible hoy en día sin la computadora y el software estadístico. (Créanme, yo crecí en la generación de la regla de cálculo.) Por fortuna, ya existen muchos paquetes de regresión excelentes, tanto para las computadoras centrales (mainframe) como para las microcomputadoras, y con el tiempo la lista crece. Los paquetes de software de regresión, como ET, LIMDEP, SHAZAM, MICRO TSP, MINITAB, EVIEWS, SAS, SPSS, BMD, STATA, Microfi t y PcGive tienen la mayoría de las técnicas econométricas y las pruebas analizadas en este libro.

En esta obra ocasionalmente pediremos al lector realizar experimentos Monte Carlo con uno o más paquetes estadísticos. Los experimentos Monte Carlo son ejercicios “divertidos” que capacitarán al lector para apreciar las propiedades de diversos métodos estadísticos analizados en este libro. Detallaremos sobre los experimentos Monte Carlo en las secciones pertinentes.

Metodología de la econometría - Requisitos matemáticos y estadísticos

 A pesar de que este libro está escrito en un nivel elemental, el autor supone que el lector conoce los conceptos básicos de la estimación estadística y las pruebas de hipótesis. Sin embargo, para quienes deseen refrescar sus conocimientos, en el apéndice A se ofrece una revisión amplia pero no técnica de los conceptos estadísticos básicos de esta obra. Respecto de las matemáticas, es deseable, aunque no esencial, estar más o menos al día con las nociones de cálculo diferencial. Si bien la mayoría de los textos universitarios de econometría emplea con libertad el álgebra matricial, deseo aclarar que este libro no la requiere. Sostengo la fi rme convicción de que las ideas fundamentales de econometría pueden transmitirse sin álgebra matricial. Sin embargo, para el benefi cio del estudiante amigo de las matemáticas, el apéndice C resume la teoría de regresión básica en notación matricial. Para estos estudiantes, el apéndice B proporciona un resumen sucinto de los principales resultados del álgebra matricial.

Metodología de la econometría - Tipos de econometría

 Como deja entrever el esquema de clasifi cación en la fi gura I.5, la econometría se divide en dos amplias categorías: econometría teórica y econometría aplicada. En cada categoría se puede tratar la materia según la tradición clásica o la bayesiana. En este libro destacamos el enfoque clásico. Para el enfoque bayesiano, el lector puede consultar las referencias al fi nal del capítulo.

La econometría teórica se relaciona con la elaboración de métodos apropiados para medir las relaciones económicas especifi cadas por los modelos econométricos. En este aspecto, la econometría se apoya en gran medida en la estadística matemática. Por ejemplo, un método muy popular en este libro es el de mínimos cuadrados. La econometría teórica debe expresar los supuestos de este método, sus propiedades y lo que les sucede cuando no se cumplen uno o más de los supuestos del método.

En la econometría aplicada utilizamos herramientas de la econometría teórica para estudiar algunos campos especiales de la economía y los negocios, como la función de producción, la función de inversión, las funciones de demanda y de oferta, la teoría de portafolio, etcétera. 

Este libro se refi ere en gran parte al desarrollo de los métodos econométricos, sus supuestos, usos y limitaciones. Ilustramos estos métodos con ejemplos en diversas áreas de la economía y los negocios. Pero éste no es un libro de econometría aplicada en el sentido de que investigue a fondo un campo particular de aplicación económica. Para esa labor existen textos especializados. Al fi nal de esta obra proporcionamos referencias de algunos de ellos.

Metodología de la econometría - Elección entre modelos rivales

 Cuando una dependencia gubernamental (digamos, el Departamento de Comercio de Estados Unidos) recopila datos económicos, como los de la tabla I.1, no necesariamente tiene una teoría económica en mente. Por tanto, ¿cómo sabe en realidad que los datos respaldan la teoría keynesiana de consumo? ¿Se debe acaso a que la función consumo keynesiana (es decir, la línea de regresión) de la figura I.3 se aproxima mucho a los puntos reales que representan a los datos? ¿Será posible que otro modelo (teoría) de consumo se ajuste igual de bien a los datos? Por ejemplo, Milton Friedman elaboró un modelo de consumo, la hipótesis de ingreso permanente.15 Robert Hall también creó un modelo de consumo, llamado hipótesis del ciclo de vida del ingreso permanente. ¿Alguno o ambos modelos pueden también ajustarse a los datos de la tabla I.1?

En resumen, la interrogante con que se enfrenta en la práctica un investigador es: ¿cómo elegir entre modelos o hipótesis que compiten entre sí, dado un fenómeno determinado, como la relación entre consumo e ingreso? Como observa Miller:

Ningún encuentro con los datos signifi ca un paso adelante hacia la confi rmación genuina, a menos que la hipótesis se las arregle mejor con esos datos que algún rival natural. . . . Lo que fortalece aquí a una hipótesis es una victoria que, al mismo tiempo, es una derrota para una posible rival.17

Entonces, ¿cómo elegir entre los varios modelos o hipótesis en disputa? Aquí Clive Granger da un consejo que vale la pena:

Me gustaría proponer que en el futuro, cuando a uno se le presente una nueva teoría o modelo empírico, se plantee las siguientes preguntas:

i) ¿Qué propósito tiene? ¿Qué tipo de decisiones económicas ayuda a tomar?

ii) ¿Existe alguna evidencia presente que me permita evaluar su calidad en comparación con teorías o modelos alternos?

Pienso que si se les da la debida atención a estos planteamientos se fortalecerá la investigación y el análisis económicos.

Conforme avancemos en este libro, saldrán al paso diversas hipótesis que compiten entre sí y que tratan de explicar varios fenómenos económicos. Por ejemplo, los estudiantes de economía conocen ya el concepto de la función producción, que representa básicamente una relación entre la producción y los insumos (capital y trabajo). En la bibliografía, dos funciones producción muy conocidas son la de Cobb-Douglas y la de elasticidad constante de sustitución. Con los datos de producción e insumos tendremos que averiguar cuál de las dos funciones producción, si acaso alguna lo hace, se ajusta bien a los datos.

La metodología econométrica clásica, consistente en los ocho pasos que acabamos de presentar, es neutral en el sentido de que sirve para probar cualquiera de estas hipótesis rivales.

¿Es posible elaborar una metodología lo bastante amplia para abarcar hipótesis contendientes? La respuesta implica un tema polémico e intrincado que analizaremos en el capítulo 13, tras entender la teoría econométrica necesaria.

Metodología de la econometría - Uso del modelo para fines de control o de políticas

 Suponga que tenemos la función keynesiana de consumo estimada dada en (I.3.3). Suponga además que el gobierno considera que un nivel de gasto de aproximadamente 8 750 (miles de millones de dólares de 2000) mantendrá la tasa de desempleo en su nivel actual de cerca de 4.2 por ciento (estimación para principios del 2006). ¿Qué nivel de ingreso garantizará la cantidad de gasto de consumo fi jado como meta?

Si los resultados de la regresión dados en la ecuación (I.3.3) parecen razonables, la aritmética simple mostrará que

8 750 = −299.5913 + 0.7218(PIB2006) (I.3.6)

que da X = 12 537, aproximadamente. Es decir, un nivel de ingresos de alrededor de 12 537 (miles de millones) de dólares, con una PMC de cerca de 0.72, producirá un gasto aproximado de 8 750 millones de dólares.

Como indican estos cálculos, un modelo estimado sirve para fi nes de control o de políticas públicas. Mediante una mezcla apropiada de política fi scal y monetaria, el gobierno puede manejar la variable de control X para producir el nivel deseado de la variable objetivo Y. La figura I.4 resume la anatomía de la creación de los modelos econométricos clásicos. 

Metodología de la econometría - Pronóstico o predicción

 Si el modelo escogido no refuta la hipótesis o la teoría en consideración, servirá para predecir el (los) valor(es) futuro(s) de la variable dependiente Y, o de pronóstico, con base en el (los) valor(es) futuro(s) conocido(s) o esperado(s) de la variable explicativa, o predictora, X.

Para ilustrarlo, suponga que queremos predecir la media del gasto de consumo para 2006. El valor del PIB para 2006 fue de 11 319.4 millones de dólares.14 Colocamos esta cifra del PIB en el lado derecho de la ecuación (I.3.3) y obtenemos:

o casi 7 870 millones de dólares. Por tanto, con ese valor del PIB, la media o el promedio del gasto de consumo previsto es de alrededor de 7 870 millones de dólares. El valor real del gasto de consumo registrado en 2006 fue de 8 044 millones de dólares. El modelo estimado (I.3.3), por tanto, subpredijo el gasto de consumo real por casi 174 000 millones de dólares. Se diría que el error de predicción es de aproximadamente 174 000 millones de dólares, que representa alrededor de 1.5% del valor real del PIB para 2006. Cuando analicemos a profundidad el modelo de regresión lineal en los siguientes capítulos, trataremos de averiguar si un error de esa naturaleza es “pequeño” o “grande”. Pero lo que ahora importa es observar que tales errores de predicción son inevitables, dada la naturaleza estadística del análisis.

Existe otro uso del modelo estimado (I.3.3). Suponga que el presidente decide proponer una reducción del impuesto sobre la renta. ¿Cuál será el efecto de dicha política en el ingreso y por consiguiente en el gasto de consumo, y a fi nal de cuentas en el empleo? Suponga que como resultado de estos cambios de política se incrementa el gasto en inversión. 

¿Cuál será el efecto en la economía? De acuerdo con la teoría macroeconómica, el cambio en el ingreso generado por un cambio equivalente a un dólar, por ejemplo, en el gasto en inversión está dado por el multiplicador del ingreso (M), el cual se define como

Si utilizamos la PMC de 0.72 obtenida en la ecuación (I.3.3), este multiplicador se convierte en

M = 3.57. Es decir, un aumento (o reducción) de un dólar en la inversión al final generará un incremento (o reducción) de más de tres veces en el ingreso; advierta que el multiplicador demora

algún tiempo en actuar.

El valor crítico en este cálculo es la PMC, pues M depende de él. Y este valor estimado de la PMC se obtiene de modelos de regresión como el de la ecuación (I.3.3). Así, un valor estimado cuantitativo de la PMC proporciona información valiosa para fi nes de políticas públicas. Al conocer la PMC, se puede predecir el curso futuro del ingreso, el gasto de consumo y el empleo que sigue a un cambio en las políticas fi scales del gobierno.

Metodología de la econometría - Pruebas de hipótesis

 En el supuesto de que el modelo ajustado sea una aproximación razonablemente buena de la realidad, tenemos que establecer criterios apropiados para comprobar si los valores estimados obtenidos en una ecuación como la (I.3.3), por ejemplo, concuerdan con las expectativas de la teoría que estamos probando. De acuerdo con los economistas “positivos”, como Milton Friedman, una teoría o hipótesis no verificable mediante la evidencia empírica no puede ser admisible como parte de la investigación científica.

Como ya señalamos, Keynes esperaba que la PMC fuera positiva pero menor que 1. En el ejemplo observamos que la PMC es alrededor de 0.72. Pero antes de aceptar este resultado como confi rmación de la teoría keynesiana de consumo, debemos averiguar si esta estimación está lo bastante abajo de la unidad para convencernos de que no se trata de un suceso debido al azar o de una peculiaridad de los datos. En otras palabras, ¿es 0.72 estadísticamente menor que 1? Si lo es, puede apoyar la teoría de Keynes.

Tal confirmación o refutación de las teorías económicas con fundamento en la evidencia muestral se basa en una rama de la teoría estadística conocida como inferencia estadística (pruebas de hipótesis). A lo largo de este libro veremos cómo realizar en la práctica este proceso de inferencia.

Metodología de la econometría - Estimación del modelo econométrico

 Ahora que tenemos los datos, la siguiente labor es estimar los parámetros de la función consumo. La estimación numérica de los parámetros da contenido empírico a la función consumo. En el capítulo 3 explicaremos el mecanismo real para estimar los parámetros. Por el momento, note que la técnica estadística conocida como análisis de regresión es la herramienta principal para obtener las estimaciones. Con esta técnica y los datos de la tabla I.1 obtuvimos los siguientes valores estimados de β1 y β2, a saber, −299.5913 y 0.7218. Así, la función consumo estimada es 

El acento circunflejo (sombrero) sobre Y indica que es un valor estimado.11 En la figura I.3 se muestra la función consumo estimada (es decir, la línea de regresión).

Como se aprecia en la fi gura I.3, la línea de regresión se ajusta bien a los datos, pues los puntos que corresponden a los datos están muy cercanos a ella. En esta gráfi ca vemos que de 1960 a 2005 el coeficiente de la pendiente (es decir, la PMC) fue de alrededor de 0.72, lo que indica que para el periodo muestral un incremento de un dólar en el ingreso real produjo, en promedio, un incremento cercano a 72 centavos en el gasto de consumo real.12 Decimos “en promedio” porque la relación entre consumo e ingreso es inexacta; como se deduce de la fi gura I.3, no todos los puntos correspondientes a los datos están exactamente en la recta de regresión. Con palabras sencillas, podemos decir que, de acuerdo con los datos, el promedio o media del gasto de consumo aumentó alrededor de 72 centavos por cada dólar de incremento en el ingreso real.

Metodología de la econometría - Obtención de información

 Para estimar el modelo econométrico dado en la ecuación (I.3.2), esto es, para obtener los valores numéricos de β1 y β2, son necesarios los datos. Aunque tendremos más que decir en el siguiente capítulo sobre la importancia crucial de los datos para el análisis económico, por el momento observemos unas cifras relacionadas con la economía de Estados Unidos de 1960 a 2005, que se presentan en la tabla I.1. La variable Y en esta tabla es el gasto de consumo personal (GCP) agregado (para la economía en su conjunto), y la variable X, el producto interno bruto (PIB), una medida del ingreso agregado, ambos medidos en miles de millones de dólares de 2000. Por consiguiente, los datos están en términos “reales”, es decir, se midieron en precios constantes (2000). Estos datos se graficaron en la figura I.3 (cf. fi gura I.2). Por el momento, haga caso omiso de la recta trazada en la figura.

Metodología de la econometría - Especificación del modelo econométrico de consumo

 El modelo puramente matemático de la función de consumo dado en la ecuación (I.3.1) es de interés limitado para el econometrista, pues supone una relación exacta o determinista entre el consumo y el ingreso. Pero las relaciones entre las variables económicas suelen ser inexactas. Así, si fuéramos a obtener información sobre gasto de consumo e ingreso disponible (es decir, después de impuestos) de una muestra de, por ejemplo, 500 familias estadounidenses y graficar estos datos, con el gasto de consumo en el eje vertical y en el eje horizontal el ingreso disponible, no esperaríamos que las 500 observaciones quedaran exactamente sobre la línea recta de la ecuación (I.3.1) porque, además del ingreso, otras variables afectan el gasto de consumo, como el tamaño de la familia, las edades de sus miembros, su religión, etcétera.

Para dar cabida a relaciones inexactas entre las variables económicas, el econometrista modificaría la función determinista de consumo en la ecuación (I.3.1) de la siguiente manera:

donde u, conocida como término de perturbación o de error, es una variable aleatoria (estocástica) con propiedades probabilísticas bien defi nidas. El término de perturbación u representa todos los factores que afectan el consumo pero que no se consideran en el modelo en forma explícita.

La ecuación (I.3.2) es un ejemplo de un modelo econométrico. Más técnicamente, dicha ecuación es un ejemplo de un modelo de regresión lineal, el principal interés de este libro. La función econométrica de consumo plantea como hipótesis que la variable dependiente Y (consumo) está relacionada linealmente con la variable explicativa X (ingreso), pero que la relación entre las dos no es exacta: está sujeta a variaciones individuales.

El modelo econométrico de la función de consumo se representa gráficamente como aparece en la figura I.2.

Metodología de la econometría - Especificación del modelo matemático de consumo

 A pesar de haber postulado una relación positiva entre el consumo y el ingreso, Keynes no especifica la forma precisa de la relación funcional entre ambas cosas. Por simplicidad, un economista matemático puede proponer la siguiente forma de la función keynesiana de consumo:

donde Y = gasto de consumo y X = ingreso, y donde β1 y β2, conocidos como los parámetros del modelo, son, respectivamente, los coefi cientes del intercepto y de la pendiente.

El coeficiente de la pendiente β2 mide la PMC. En la fi gura I.1 se presenta geométricamente la ecuación (I.3.1). Esta ecuación plantea que el consumo está relacionado linealmente con el ingreso, y es un ejemplo de un modelo matemático de la relación entre consumo e ingreso, llamada en economía función consumo. Un modelo es simplemente un conjunto de ecuaciones matemáticas. Si el modelo tiene una sola ecuación, como en el ejemplo anterior, se denomina modelo uniecuacional, mientras que si tiene más de una ecuación, se conoce como modelo multiecuacional (consideraremos más adelante este tipo de modelos).

En la ecuación (I.3.1), la variable que aparece al lado izquierdo del signo de la igualdad se llama variable dependiente, y la(s) variable(s) del lado derecho se llama(n) variable(s) independiente(s), o explicativa(s). Así, en la función keynesiana de consumo, la ecuación (I.3.1), el consumo (gasto) es la variable dependiente, y el ingreso, la explicativa.

Metodología de la econometría - Planteamiento de la teoría o hipótesis

 Keynes plantea:

La ley psicológica fundamental… consiste en que los hombres [y las mujeres], como regla general y en promedio, están dispuestos a incrementar su consumo a medida que aumenta su ingreso, pero no en la misma cuantía del aumento en su ingreso.

En pocas palabras, Keynes postula que la propensión marginal a consumir (PMC), es decir, la tasa de cambio del consumo generado por una unidad (digamos, un dólar) de cambio en el ingreso, es mayor que cero pero menor que uno.

Metodología de la econometría

 ¿Cómo proceden los econometristas en el análisis de un problema económico? Es decir, ¿cuál es su metodología? Aunque existen diversas escuelas de pensamiento sobre metodología econométrica, aquí presentaremos la metodología tradicional o clásica, que aún predomina en la investigación empírica en economía y en las ciencias sociales y del comportamiento. 

En términos generales, la metodología econométrica tradicional se ajusta a los siguientes lineamientos:

1. Planteamiento de la teoría o de la hipótesis.

2. Especifi cación del modelo matemático de la teoría.

3. Especifi cación del modelo econométrico o estadístico de la teoría.

4. Obtención de datos.

5. Estimación de los parámetros del modelo econométrico.

6. Pruebas de hipótesis.

7. Pronóstico o predicción.

8. Utilización del modelo para fi nes de control o de políticas.

Para ilustrar estos pasos, consideremos la conocida teoría keynesiana de consumo.

Econometria ¿Por qué una disciplina aparte?

 Como indican las defi niciones anteriores, la econometría es una amalgama de teoría económica, economía matemática, estadística económica y estadística matemática. Aun así, la materia merece un estudio separado por las siguientes razones.

La teoría económica hace afi rmaciones o formula hipótesis de naturaleza sobre todo cualitativa. Por ejemplo, la teoría microeconómica establece que, si no intervienen otros factores, se espera que la reducción del precio de un bien aumente la cantidad demandada de ese bien. Así, la teoría económica postula una relación negativa o inversa entre el precio y la cantidad demandada de un bien. Pero la teoría por sí sola no proporciona medida numérica alguna de la relación entre los dos; no dice cuánto aumentará o se reducirá la cantidad como resultado de un cambio determinado en el precio del bien. El trabajo del econometrista es proporcionar tales estimaciones numéricas. En otras palabras, la econometría da contenido empírico a gran parte de la teoría económica.

El interés principal de la economía matemática es expresar la teoría económica en una forma matemática (ecuaciones) sin preocuparse por la capacidad de medición o de verifi cación empírica de la teoría. La econometría, como ya apuntamos, se interesa sobre todo en la verifi cación empírica de la teoría económica. Como veremos, el econometrista suele emplear ecuaciones matemáticas, propuestas por el economista matemático, pero las expresa de forma que se presten para la prueba empírica. Y esta conversión de ecuaciones matemáticas en ecuaciones econométricas requiere una gran dosis de ingenio y destreza.

La estadística económica se relaciona en primer lugar con la recopilación, procesamiento y presentación de cifras económicas en forma de gráfi cos y tablas. Éste es el trabajo del estadístico económico, cuya actividad principal consiste en recopilar cifras sobre el producto nacional bruto (PNB), empleo, desempleo, precios, etc. Los datos así reunidos constituyen la materia prima del trabajo econométrico. Pero el estadístico económico no va más allá de la recolección de información, pues no le conciernen las cifras recopiladas para probar las teorías económicas. Sin duda, es el econometrista quien se ocupa de realizar esta labor.

Aunque la estadística matemática proporciona muchas herramientas para esta ciencia, el econometrista a menudo necesita métodos especiales por la naturaleza única de la mayoría de las cifras económicas, pues no se generan como resultado de un experimento controlado. El econometrista, como el meteorólogo, suele depender de cifras que no controla directamente. Como observa Spanos, acertadamente:

En econometría, el que construye el modelo a menudo se enfrenta a datos provenientes de la observación más que de la experimentación. Esto tiene dos implicaciones importantes para la creación empírica de modelos en econometría. Primero, se requiere que quien elabore modelos domine muy distintas habilidades en comparación con las que se necesitan para analizar los datos experimentales… Segundo, la separación de quien recopila los datos y el analista exige que quien elabora modelos se familiarice por completo con la naturaleza y la estructura de los datos en cuestión.

¿Qué es la econometría?

En términos literales econometría signifi ca “medición económica”. Sin embargo, si bien es cierto que la medición es una parte importante de la econometría, el alcance de esta disciplina es mucho más amplio, como se deduce de las siguientes citas:

• La econometría, resultado de cierta perspectiva sobre el papel que desempeña la economía, consiste en la aplicación de la estadística matemática a los datos económicos para dar soporte empírico a los modelos construidos por la economía matemática y obtener resultados numéricos.
• . . . la econometría puede definirse como el análisis cuantitativo de fenómenos económicos reales, basados en el desarrollo simultáneo de la teoría y la observación, relacionados mediante métodos apropiados de inferencia.
• La econometría se defi ne como la ciencia social en la cual las herramientas de la teoría económica, las matemáticas y la inferencia estadística se aplican al análisis de los fenómenos económicos. 
• La econometría tiene que ver con la determinación empírica de las leyes económicas. 
• El arte del econometrista consiste en encontrar un conjunto de supuestos lo bastante específi cos y realistas para que le permitan aprovechar de la mejor manera los datos con que cuenta.
• Los econometristas… son una ayuda decisiva en el esfuerzo por disipar la mala imagen pública de la economía (cuantitativa o de otro tipo) considerada como una materia en la cual se abren cajas vacías, suponiendo la existencia de abrelatas, para revelar un contenido que diez economistas interpretarán de 11 maneras diferentes.
• El método de la investigación econométrica busca en esencia una conjunción entre la teoría económica y la medición real, con la teoría y la técnica de la inferencia estadística como puente.

Dawn C. Porter

 Dawn Porter ha sido profesora adjunta del Departamento de Administración de Operaciones de la Marshall School of Business de la University of Southern California (USC) desde el otoño de 2006. En la actualidad imparte clases de introducción a la estadística tanto en licenciatura como en maestría en la Escuela de Administración. Antes de incorporarse al cuerpo docente de la USC, de 2001 a 2006, Dawn fue profesora adjunta de la McDonough School of Business en la Georgetown University, y antes de eso fue profesora visitante del Departamento de Psicología de la Graduate School of Arts and Sciences en la New York University (NYU). En NYU impartió diversos cursos sobre métodos estadísticos avanzados y también fue profesora de la Stern School of Business. Obtuvo su doctorado en Estadística en la Stern School.

Las áreas de interés para la investigación de Dawn son análisis categórico, medidas de acuerdo, creación de modelos multivariados y aplicaciones en el campo de la psicología. Su investigación actual examina los modelos de subasta en internet desde una perspectiva estadística. Ha presentado sus estudios de investigación en las conferencias de Joint Statistical Meetings, las reuniones del Decision Sciences Institute, la Conferencia Internacional sobre Sistemas de Información, varias universidades, como la London School of Economics y NYU, así como en diversas series de seminarios sobre comercio electrónico y estadística. Dawn es también coautora de Essentials of Business Statistics, 2a. edición, McGraw-Hill/Irwin, 2008. Fuera del ámbito académico, Dawn fue contratada como consultora en estadística de KPMG, Inc. También trabajó como consultora en estadística para muchas otras empresas importantes, entre otras, Ginnie Mae, Inc., Toys R Us Corporation, IBM, Cosmaire, Inc., y New York University (NYU) Medical Center.

Damodar N. Gujarati

Después de enseñar durante más de 25 años en la City University of New York y 17 años en el Departamento de Ciencias Sociales de la U.S. Military Academy en West Point, Nueva York, el doctor Gujarati es actualmente profesor emérito de economía de la Academia. El doctor Gujarati recibió el grado de M.Com de la Universidad de Bombay en 1960, el grado de M.B.A. de la Universidad de Chicago en 1963 y el grado de Ph.D. de la Universidad de Chicago en 1965. El doctor Gujarati ha publicado una gran cantidad de trabajos en reconocidas revistas nacionales e internacionales, como Review of Economics and Statistics, Economic Journal, Journal of Financial and Quantitative Analysis y Journal of Business. El doctor Gujarati fue miembro del Consejo Editorial de Journal of Quantitative Economics, publicación ofi cial de la Sociedad Econométrica de India. El doctor Gujarati es también autor de Pensions and the New York Fiscal Crisis (The American Enterprise Institute, 1978), Government and Business (McGraw-Hill,

1984) y Essentials of Econometrics (McGraw-Hill, 3a. ed., 2006). Los libros del doctor Gujarati sobre econometría se han traducido a diversos idiomas.

El doctor Gujarati fue profesor visitante de la Universidad de Sheffi eld, Inglaterra (1970- 1971), profesor visitante Fulbright en India (1981-1982), profesor visitante en la Facultad de Administración de la Universidad Nacional de Singapur (1985-1986) y profesor visitante de econometría de la Universidad de Nueva Gales del Sur, Australia (durante el verano de 1988). El doctor Gujarati ha dictado numerosas conferencias sobre temas micro y macroeconómicos en países como Australia, China, Bangladesh, Alemania, India, Israel, Mauricio y la República de Corea del Sur.

Modelo TOBIT Parte 2

¿Es posible estimar la regresión (16.14.1) utilizando solamente n1 observaciones y simplemente no preocuparse por las n2 observaciones restantes? La respuesta es no, ya que las estimaciones MCO de los parámetros obtenidos del subconjunto de n1 observaciones estaran sesgadas y serán inconsistentes.

Para ver esto, considérese la figura 16.7. Como lo muestra esta figura, si Y no es observado, todas esas observaciones (= n2) quedaran sobre el eje horizontal. Si Y es observado, las observaciones (= n1)  quedaran en el plano Y-X. Es intuitivamente claro que si se estima una regresion basada en las n1 observaciones solamente, los coeficientes resultantes del intercepto y de la pendiente estan limitados a ser diferentes de los que se obtendrian si todas las n1 + n2 observaciones fueran tenidas en cuenta.

¿Cómo se estiman entonces los modelos de regresién tobit (o censurados), tales como (16.14.1)?

No se trabajará en los cálculos matematicos pero, para estimar los parámetros de tales modelos puede utilizarse el método de maxima verosimilitud (véase el capitulo 4). La mayoria de los paquetes de computador mas comunes, tales como ET, SHAZAM y RATS, tienen ahora programas para estimar los modelos tobit. Se presentara ahora un ejemplo ilustrativo.

Modelo TOBIT

Una extensión del modelo probit es el modelo tobit, desarrollado por James Tobin, economista laureado con el Nobel. Para explicar este modelo, se contintia con el ejemplo de propiedad de vivienda. Pero supéngase que ahora se desea encontrar la cantidad de dinero que el consumidor gasta en omprar una casa en relacién con su ingreso (y otras variables econdmicas). Ahora se tiene roblema: Si un consumidor no compra una casa, obviamente no se tiene información sobre el gasto en vivienda de tales consumidores; se tiene tal informacion solamente sobre los consumidores que efectivamente compran casa.

Asi, los consumidores estén divididos en dos grupos, uno que consiste, consumidores sobre quienes se posee informacién sobre los regresores (por

de interés hipotecaria, etc) al igual que sobre la variable regresada (cantidad de gasto en vivienda) y otro que consiste, por ejemplo, en n2 consumidores sobre quienes solamente se tiene información sobre los regresores pero no sobre la variable regresada. Cuando en una muestra la información sobre la variable regresada esté disponible solamente para algunas observaciones, está se conoce como muestra censurada. Por  consiguiente, el modelo tobit también se conoce como un modelo de regresión censurada. Algunos autores llaman a tales modelos modelos de variable dependiente limitada  debido a la restriccién impuesta sobre los valores tomados por la variable regresada. 

En términos matemáticos, se puede expresar el modelo tobit como:

donde RHS =  lado derecho. Nota: Otras variables X pueden agregarse fácilmente al modelo.