Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 4

 Un monopolista que puede fi jar el precio o la producción (pero no ambos factores) tal vez desee conocer la demanda de un producto con diversos precios. Tal experimento permite estimar la elasticidad del precio (es decir, la respuesta a variaciones del precio) de la demanda del producto y permite determinar el precio que maximiza las ganancias.

Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 3

 3. Al considerar lo referente a la economía, a un economista quizá le interese estudiar la dependencia del consumo personal respecto del ingreso personal neto disponible (después de impuestos). Con un análisis de este tipo se calcula la propensión marginal a consumir (PMC), es decir, el cambio promedio del consumo ante un cambio, digamos, de un dólar en el ingreso real (ver la figura 1.3).

Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 2

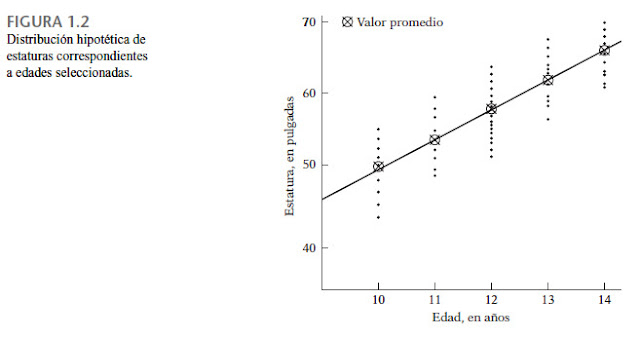
 2. Considere el diagrama de dispersión en la figura 1.2, que presenta la distribución de una población hipotética de estaturas de niños en edades fijas. Observe que existe un rango (distribución) de estaturas correspondiente a cada edad. Es obvia la improbabilidad de que todos los niños de una edad determinada tengan estaturas idénticas. Pero, en promedio, la estatura se incrementa con la edad (por supuesto, hasta cierta edad), que se ve con claridad al trazar una recta (la recta de regresión) por los puntos dentro de los círculos, los cuales representan la estatura promedio de determinadas edades. Por consiguiente, si se conoce la edad, se predice la estatura promedio de dicha edad mediante la recta de regresión.

Naturaleza del análisis de regresión - Interpretación moderna de la regresión - Ejemplo 1

 Considere de nuevo la ley de regresión universal de Galton. A él le interesaba averiguar las razones de la estabilidad en la distribución de estaturas dentro de una población. En el enfoque moderno, la preocupación no es esta explicación, sino averiguar cómo cambia la estatura promedio de los hijos dada la estatura de los padres. En otras palabras, lo que interesa es predecir la estatura promedio de los hijos a partir de la estatura de sus padres. Para ver cómo hacerlo, considere la figura 1.1, que corresponde a un diagrama de dispersión. La fi gura muestra la distribución de las estaturas de los hijos en una población hipotética, correspondiente al conjunto de valores dados o fijos de las estaturas de los padres. Observe que, para cualquier estatura de un padre, existe un rango (distribución) de estaturas de los hijos. Sin embargo, observe también que, a pesar de la variabilidad de la estatura de los hijos conforme al valor de la estatura de los padres, la estatura promedio de los hijos aumenta, por lo general, en la medida en que lo hace la estatura de los padres. Para demostrar esto con claridad, las cruces dentro de los círculos en la figura indican la estatura promedio de los hijos que corresponde a una estatura determinada de los padres. Estos promedios se conectan para obtener la línea recta de la fi gura. Esta línea, como veremos, se conoce como recta de regresión. Dicha recta muestra que el promedio de la estatura de los hijos aumenta conforme crece la de los padres.

Naturaleza del análisis de regresión - Interpretación moderna de la regresión

 La interpretación moderna de la regresión es, sin embargo, muy diferente. En términos generales, se afirma que:

El análisis de regresión trata del estudio de la dependencia de una variable (variable dependiente) respecto de una o más variables (variables explicativas) con el objetivo de estimar o predecir la media o valor promedio poblacional de la primera en términos de los valores conocidos o fi jos (en muestras repetidas) de las segundas.

La importancia trascendental de este enfoque del análisis de regresión se verá claramente sobre la marcha, pero algunos ejemplos sencillos aclararán este concepto básico.

Naturaleza del análisis de regresión - Origen histórico del término regresión

 Francis Galton acuñó el término regresión. En un famoso ensayo, Galton planteó que, a pesar de la tendencia de los padres de estatura alta a procrear hijos altos y los padres de estatura baja, hijos bajos, la estatura promedio de los niños de padres de una estatura determinada tendía a desplazarse, o “regresar”, a la estatura promedio de la población total.1 En otras palabras, la estatura de los hijos de padres inusualmente altos o inusualmente bajos tiende a dirigirse a la estatura promedio de la población. La ley de regresión universal de Galton fue confi rmada por su amigo Karl Pearson, quien reunió más de mil registros de estaturas de miembros de grupos familiares. Pearson descubrió que la estatura promedio de los hijos de un grupo de padres de estatura alta era menor que la estatura de sus padres, y que la estatura promedio de los hijos de un grupo de padres de estatura baja era mayor que la estatura de sus padres; es decir, se trata de un fenómeno mediante el cual los hijos altos e hijos bajos “regresan” por igual a la estatura promedio de todos los demás. En palabras de Galton, se trata de una “regresión a la mediocridad”.

Naturaleza del análisis de regresión

 Como se mencionó en la introducción, la regresión es una herramienta fundamental de la econometría; en este capítulo se considera muy brevemente la naturaleza de este instrumento.