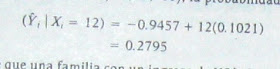Busca en el Blog
jueves, 18 de agosto de 2016
Modelo LOGIT: Ejemplos Ilustrativos "Una aplicación del análisis Logit a la predicción de blancos de fusión"
miércoles, 17 de agosto de 2016
Modelo LOGIT: Ejemplo Numérico (VI)
miércoles, 3 de agosto de 2016
Modelo LOGIT: Ejemplo Numérico (V)
Retornando a la regresión (16.9.1), se observa que los coeficientes estimados individualmente son estadísticamente significativos aun al nivel del 1%. Pero, como se advirtió anteriormente, esta afirmación es correcta, estrictamente, en muestras grandes, es decir, cuando el número de observaciones Ni para cada Xi es grande -no es preciso que el número de niveles al cual se mide Xi sea necesariamente grande; en el ejemplo, X tiene 10 valores diferentes.
Al examinar la tabla 16.5, se observa que las Ni, aunque no son muy grandes, son razonablemente grandes, pero téngase en mente que entre más grandes sean las Ni, mejores serán los procedimientos de prueba.
El R² estimado es bastante "alto", alrededor de 0.96. Pero se ha señalado que en modelos de variables dependiente dicótoma, el R² como medida de bondad del ajuste es de valor cuestionable. En la literatura se han sugerido diversas alternativas pero éstas no se considerarán aquí.
martes, 2 de agosto de 2016
Modelo LOGIT: Ejemplo Numérico (IV)
lunes, 1 de agosto de 2016
Modelo LOGIT: Ejemplo Numérico (III)
domingo, 31 de julio de 2016
sábado, 9 de julio de 2016
Modelo LOGIT: Ejemplo Numérico (II)
viernes, 8 de julio de 2016
Modelo LOGIT: Ejemplo Numérico (I)
jueves, 7 de julio de 2016
Estimación del modelo LOGIT (VIII)
miércoles, 6 de julio de 2016
Estimación del modelo LOGIT (VII)
martes, 5 de julio de 2016
lunes, 4 de julio de 2016
Estimación del modelo LOGIT (V)
domingo, 3 de julio de 2016
Estimación del modelo LOGIT (IV)
sábado, 2 de julio de 2016
Estimación del modelo LOGIT (III)
lo cual será una estimación relativamente buena del verdadero logit Li si el número de observaciones Ni a cada nivel Xi es razonablemente grande.
miércoles, 29 de junio de 2016
Estimación del modelo LOGIT (II)
Pero supóngase que se tiene la información, como se muestra en la tabla 16.4. Correspondiente a cada nivel de ingreso X, en esta tabla son Ni familias, de las cuales ni poseen casa (ni ≤ Ni). Por consiguiente, si ahora se calcula.
martes, 28 de junio de 2016
Estimación del modelo LOGIT (I)
En breve, se analizarán las propiedades del término de perturbación estocástico.
Para estimar el modelo, además de Xi, se necesitan los valores de logit Li. Pero ahora se incurre en algunas dificultades. Si existe información disponible sobre familias individuales, como en la tabla 16.1., entonces Pi = 1 si una familia posee una casa y Pi = 0 si no la posee. Pero si se colocan estos valores directamente en el logit Li, se obtiene.
lunes, 20 de junio de 2016
El modelo Logit (VI)
5. Mientras que el MLP supone que Pi está linealmente relacionado con Xi, el modelo logit supone que el algoritmo de la razón de probabilidades está relacionado linealmente con Xi.
domingo, 19 de junio de 2016
El modelo Logit (V)
sábado, 18 de junio de 2016
El modelo Logit (IV)
- A medida que P va de 0 a 1 (es decir, a medida que Z varía de -∞ a + ∞, el logit L va de -∞ a + ∞. Es decir, aunque las probabilidades (por necesidad) se enceuntran entre 0 y 1, los logit no están limitados en esa forma.
- Aunque L es lineal en X, las probabilidades en sí mismas no lo son. Esta propiedad hace contraste con el modelo MLP (16.7.1) en donde las probabilidades aumentan linealmente con X^18
viernes, 17 de junio de 2016
El modelo Logit (III)
Ahora, si se toma el logartimo natural de (16.7.5), se obtiene un resultado muy interesante, a saber
jueves, 16 de junio de 2016
El modelo Logit (II)
Es fácil verificar que a medida que Zi se encuentra dentro de un rango de -∞ a + ∞ , Pi se encuentra dentro de un rango de 0 a 1 y que Pi no está linealmente relacionado con Zi (es decir, con Xi), satisfaciendo así los dos requerimientos considerados anteriormente. Pero parece que al satisfacer estos requerimientos, se ha creado un problema de estimación porque Pi es no lineal no solamente en X sino tambien en los β, como puede verse claremente a partir de (16.7.2). Esto significa que no se puede utilizar el procedimiento familiar MCO para estimar los parámetros. Pero este problema es más aparente que real porque (16.7.2) es intrínsecamente lineal, lo cual puede verse de la siguiente manera.
Si Pi, la probabilidad de poseer una casa, está dada por (16.7.3), entonces (1-Pi), la probabilidad de no poseer una casa es
miércoles, 15 de junio de 2016
El modelo Logit (I)
martes, 14 de junio de 2016
Alternativas al MLP (IV)
Aunque el análisis detallado de los modelos logit y probit está por fuera del alcance de este libro, se indicará de manera algo informal la forma de estimar tales modelos y la forma de interpretarlos.
domingo, 12 de junio de 2016
Alternativas al MLP (III)
Geomeétricamente, el modelo que se desea tendría la forma de la figura 16.2. Obsérvese en este modelo que la probabilidad se encuentra entre 0 y 1 y que éste varía en forma no lineal con X.
sábado, 11 de junio de 2016
Alternativas al MLP (II)
viernes, 10 de junio de 2016
Alternativas al MLP (I)
Como se ha visto, el MLP tiene infidad de problemas, tales como (1) la no normalidad de los ui, (2) la heteroscedasticidad de ui, (3) la posibilidad de que Yi se encuentre por fuera del rango 0-1 y (4) los valores generalmente bajos de R². Pero estos problemas se pueden resolver. Por ejemplo, se puede utilizar el MCP para resolver el problema de heteroscedasticidad o incrementar el tamaño de la muestra y minimizar así el problema de la no normalidad. Recurriendo a las técnicas de mínimos cuadrados restringidos o de programación matemática, es posible hacer que las posibilidades estimadas se encuentren dentro del intervalo 0-1.
jueves, 9 de junio de 2016
Aplicaciones de MLP - Ejemplo Predicción de omisiones en el pago de bonos (II)
Donde P = 0 si la comunidad incumplió el pago y de lo contrario, IMPUESTO = tasas de impuesto promedio de 1929, 1930 y 1931: INT = % del presupuesto observado asignado a pagos de interés en 1930; AV = Crecimiento porcentual en los avalúos catastrales de la propiedad entre 1925 y 1930; DAV = razón de la deuda neta directa total con respecto al avalúo catastral total en 1930; y BIENESTAR = porcentaje del presupuesto de 1930 asignado a caridad, pensiones y beneficios de los soldados.
La interpretación de (16.5.2) nuevamente es clara. Así, manteniendo las otras condiciones iguales, un incremento en la tasa de impuestos de US$1 por cada mil aumentará la probabilidad de incumplimiento en alrededor de 0.03, o 3%. El valor de R² es relativamente bajo pero, como se mencionó anteriormente, en los MLP, los valores de R² generalmente tienden a ser inferiores y son de uso limitado al juzgar la bondad de ajustes del modelo.
miércoles, 8 de junio de 2016
Aplicaciones de MLP - Ejemplo Predicción de omisiones en el pago de bonos (I)
martes, 7 de junio de 2016
Aplicaciones de MLP - Ejemplo Predicción de las tasas de bonos (II)
La interpretación de la regresión es clara. Por ejemplo, el 0.0486 asociado con X3 significa que, manteniendo las otras condiciones iguales, un incremento de un punto porcentual en la tasa de rendimiento conducirá, en promedio, a alrededor de un 0.05 de incremento en la probabilidad de que un bono obtenga la clasificación Aa. En forma similar, cuanto más alta sea la tasa de endeudamiento elevada al cuadrado, menor en 0.02 será la probabilidad de que un bono sea clasificado como bono Aa por unidad de incremento en esta tasa.
domingo, 5 de junio de 2016
Aplicaciones de MLP - Ejemplo Predicción de las tasas de bonos (I)
sábado, 4 de junio de 2016
Aplicaciones de MLP - Estudio de Cohen, Rea y Lerman (IV)
Ahora, considérese el término de interacción estado civil y edad. La tabla muestra que la probabilidad de participación en la fuerza laboral es más alta en cerca de 29% para aquellas mujeres solteras (comparado con la categoría base) y es más baja en alrededor de 28% para aquellas mujeres de 65 y más años de edad (nuevamente en relación con la categoría base). Pero la probabilidad de participación de mujeres solteras y que tienen 65 años o más a menor en cerca de 20% compara con la categoría base. Esto implica que es probable que las mujeres solteras de 65 años de edad y más participen en la fuerza laboral en mayor proporción que aquellas casadas o clasificadas dentro de la categoría "otros", con 65 años de edad.
Siguiendo este procedimient, el lector puede interpretar fácilmente el resto de los coeficientes dados en la tabla 16.3. De la información dada, es fácil obtener las estimaciones de las probabilidades condicionales de la participación de la fuerza laboral de las diversas categorías. Así, si se desea encontrar la probabilidad para mujeres casadas (otras), entre las edades de 22 a 54, con 12 a 15 años de educación, con una tasa de desempleo de 2.4 a 3.4%, cambio de empleo de 3.5 a 6.49%, oportunidades relativas de empleo de 74% y por encima y con IFMJ de US$7500 y más se obtiene
0.4368 + 0.1523 + 0.2231 + 0.0213 + 0.0301 + 0.0571 - 0.2455 = 0.6326
En otras palabras, la probabilidad de la participación de las mujeres en la fuerza laboral, con las características anteriores se ha estimado en alrededor del 63%.
viernes, 3 de junio de 2016
Aplicaciones de MLP - Estudio de Cohen, Rea y Lerman (III)
Retornando a la interpretación de los resultados, se observa que cada coeficiente de pendiente de la tasa de cambio en la probabilidad condicional del evento que está ocurriendo ante un cambio unitario en el valor de la variable explicativa. Por ejemplo, el coeficiente de -0.2753 que acompaña a la variable "edad 65 y más" significa que, manteniendo todos los demás factores constantes, la probabilidad de participación en la fuerza laboral de mujeres con edades entre 22 y 54 años). Utilizando el mismo razonamiento, el coeficiente de 0.3061, asociado con la variable "16 o más años de educación", significa que manteniendo todos los demás factores constantes, la probabilidad de que las mujeres con esta misma educación participen en la fuerza laboral es más alta en cerca del 31% (comparado con la categoría base, que son mujeres con menos de 5 años de educación.)
jueves, 2 de junio de 2016
miércoles, 1 de junio de 2016
Aplicaciones de MLP - Estudio de Cohen, Rea y Lerman (II)
Antes de interpretar los resultados, obsérvese estas características: la regresión anterior fue estimada utilizando MCO. Para corregir por heteroscedasticidad, los autores utilizaron el procedimiento de dos etapas descrito anteriormente en algunas de sus regresiones pero encontraron que los errores estándar de las estimaciones así obtenidas no diferían materialmente de las obtenidas sin la corrección por heteroscedasticidad. Posiblemente, este resultado se deba al puro tamaño de la muestra, de alrededor de 25,000. Debido a este gran tamaño de muestra, los valores t estimados pueden ser probados por su significancia estadística mediante el procedimiento MCO usual aun cuando el término de error adquiera valores dicotómicos. El R² estimado de 0.175 puede parecer relativamente bajo, pero en vista del gran tamaño de la muestra, este R² sigue siendo significativo con base en la prueba F dada en la sección 8.5. Finalmente, obsérvese la forma como los autores han mezclado variables cuantitativas y cualitativas y cómo han tomado en consideración los efectos de la interacción.
martes, 31 de mayo de 2016
Aplicaciones de MLP - Estudio de Cohen, Rea y Lerman (I)
sábado, 28 de mayo de 2016
Aplicaciones de MLP
viernes, 27 de mayo de 2016
MLP: Un ejemplo númerico (V)
jueves, 4 de febrero de 2016
MLP: Un ejemplo númerico (IV)
miércoles, 3 de febrero de 2016
MLP: Un ejemplo númerico (III)
miércoles, 20 de enero de 2016
MLP: Un ejemplo númerico (II)
martes, 19 de enero de 2016
MLP: Un ejemplo númerico (I)
domingo, 17 de enero de 2016
Problemas en la estimación de MLP - R², Valor cuestionable como medida de bondad del ajuste
Por estas razones, John Aldrich y Forrest Nelson sostienen que "el uso del coeficiente de determinación como estadístico resumen debe evitarse en modelos con variable dependiente cualitativa."
sábado, 16 de enero de 2016
Problemas en la estimación de MLP - No cumplimiento de 0 ≤ E(Yi| Xi) ≤ 1
viernes, 15 de enero de 2016
Problemas en la estimación de MLP - Varianzas heteroscedásticas de las perturbaciones (IV)
Etapa 1
Efectúese la regresión MCO sobre (16.2.1) sin considerar el problema de heteroscedasticidad y obténgase Yi = el valro estimado de la verdadera E(Yi|Xi). Luego, obténgase wi = Yi(1-Yi), el valor estimado de wi.Etapa 2
Utilícese el wi estimado para transformar la información como en (16.3.5) y efectúese la regresión MCO sobre la informaci;on así transformada.jueves, 14 de enero de 2016
Problemas en la estimación de MLP - Varianzas heteroscedásticas de las perturbaciones (III)
miércoles, 13 de enero de 2016
Problemas en la estimación de MLP - Varianzas heteroscedásticas de las perturbaciones (II)
donde se hace uso del hecho de que E(Yi|Xi) = β1 + β2Xi = Pi. La ecuación (16.3.4) muestra que la varianza de ui es heteroscedástica porque depende de la esperanza condicional de Y, la cual, por supuesto, depende del valor que adquiera X. Así, en última instancia, la varianza de ui depende de X y, por tanto no es homoscedástica.
martes, 12 de enero de 2016
Problemas en la estimación de MLP - Varianzas heteroscedásticas de las perturbaciones (I)
lunes, 11 de enero de 2016
Problemas en la estimación de MLP - No normalidad de las perturbaciones ui (II)
Obviamente, no puede suponerse que ui, esté normalmente distribuida; en realidad ésta sigue un distribución binomial.
Pero el no cumplimiento del supuesto de normalidad puede no ser tan crítico como parece porque se sabe que las estimaciones puntuales MCO aún permanecen insesgadas (recuérdese que si el objetivo es la estimación puntual, el supuesto de normalidad es inconsecuente). Además, puede demostrarse que a medida que el tamaño de la muestra aumenta indefinidamente, los estimadores MCO generalmente tienden a estar normalmente distribuidos. Por consiguiente, en muestras grandes, la inferencia estadística del MLP seguirá el procedimiento MCO usual bajo el supuesto de normalidad.
domingo, 10 de enero de 2016
Problemas en la estimación de MLP - No normalidad de las perturbaciones ui (I)
sábado, 9 de enero de 2016
Problemas en la estimación de MLP
viernes, 8 de enero de 2016
Modelo lineal de probabilidad (MLP) (III)
es decir, la esperanza condicional o probabilidad condicional debe encontrarse entre 0 y 1.
miércoles, 6 de enero de 2016
Modelo lineal de probabilidad (MLP) (II)
Suponiendo que E(ui) = 0, como es lo usual (para obtener estimadores insesgados), se obtiene:
E(Yi| Xi) = β1 + β2Xi