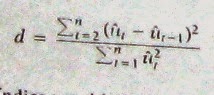Prueba RESET de Ramsey (I)

Ramsey ha propuesto una prueba general de errores de especificación conocida como RESET (Prueba de error de especificación en regresión). Aquí se ilustrará solamente la versión más simple de la prueba. Para establecer los conceptos, se continúa con el ejemplo costo-producción y se supone que la función de costos es lineal en la producción de la siguiente forma

El estadístico d de Durbin-Watson una vez más (IV)

En el ejemplo de costos, la variable Z(=X) (producción) ya fue ordenada. Por consiguiente, no es preciso calcular el estadístico d nuevamente. Como se ha visto, el estadístico d para las funciones de costo lineal y cuadrática sugiere la presencia de errores de especificación. Los remedios son claros: Introdúzcanse los términos cuadrático y cubico en la función lineal de costos y el término cúbico en la función cuadrática de costos. En resumen efectúese la regresión del modelo cúbico de costo.

El estadístico d de Durbin-Watson una vez más (III)

Para aplicar la prueba de Durbin-WAtson para detectar error (o errores) de especificación de un modelo, se procede de la siguiente manera:
1. A partir de un modelo supuesto, obténgase los residuales MCO.
2. Si se cree que el modelo supuesto está mal especificado porque excluye una variable explicativa relevante, por ejemplo, Z, ordénese los residuales obtenidos en el paso 1 de acuerdo con los valores crecientes de Z. Nota: La variable Z podría ser una de las variables X incluidas con el modelo supuesto o podría ser algún tipo de función de esa variable. tal como X² o X³.
3. Calcúlese el estadístico d con los residuales así ordenados mediante la fórmula d usual, a saber.

Nota: En este contexto, el subíndice t es el índice de la observación que no necesariamente se refiere a una serie de tiempo.

4. Con base en las tablas de Durbin-WAtson, si el valor d estimado es significativo, entonces se puede aceptar la hipótesis de mala especificación del modelo. Si ese resulta ser el caso, las medidas remediables surgirán naturalmente por si mismas.

El estadístico d de Durbin-Watson una vez más (II)

La "correlación" positiva observada en los residuales cuando se ajusta el modelo lineal o cuadrático no es una medida de correlación serial (de primer orden) sino el error (o errores) de especificación (del modelo). La correlación observada refleja simplemente el hecho de que hay una o más variables pertenecientes al modelo que están incluidas en el término de error y necesitan ser desechadas de éste y ser introducidas, por derecho propio, como variables explicativas: Si se excluye X²i de la función de costos, entonces, como lo muestra (13.2.3), el término de error en el modelo mal especificado (13.2.2) es, en realidad, (u1i β4X³i) el  cual presentará un patrón sistemático (por ejemplo, de autocorrelación positiva) si en realidad X³i afecta a Y significativamente.

El estadístico d de Durbin-Watson una vez más (I)

Si se examina el d de Durbin-Watson que aparece en la tabla 13.1., se observa que para la función lineal de costos, el d estimado es 0.716, lo cual sugiere que hay "correlación" positiva en los residuales estimados: para n= 10 y  k'= 1, los valores d críticos al 5% son dL = 0.879 y du = 1.320. De la misma manera, el valor d calculado para la función cuadrática de costo es 1.038, mientras que los valores críticos al 5% son dL = 0.967 y du = 1.641, indicando indecisión. Pero, si se utiliza la prueba d modificada, se puede decir que hay "correlación" positiva en los residuales, ya que el d calculado es menor que du. Para la función cúbica de costo, la verdadera especificación, el valor d estimado no indica "correlación" positiva alguna en los residuales.

Examen de los residuos (II)

Aunque se sabe que ambos investigadores han cometido errores de especificación, para fines pedagógicos véase cómo se comportan los residuales estimados en los tres modelos. (La información costo-producción está dada en la tabla 7.4). La figura 13.1 habla por sí misma: A medida que uno se mueve de izquierda a derecha, es decir, a medida que uno se acerca a la verdad, no solamente los residuales son más pequeños (en valor absoluto) sino también estos no presentan los giros cíclicos pronunciados asociados con modelos mal especificados.

La utilidad de examinar la gráfica de residuales es entonces clara: Si hay errores de especificación, los residuales presentarán patrones distinguibles.

Examen de los residuos (I)

Como se anotó en el cap 12, el examen de los residuos es un buen diagnóstico visual para detectar la autocorrelación o la heteroscedasticidad. Pero estos residuales pueden también ser examinados, especialmente en información de corte transversal, para detectar errores de especificación en los modelos, tales como la omisión de una variable importante o la definición de una forma funcional incorrecta. Si en realidad tales errores existen, una gráfica de los residuales permitirá apreciar los patrones distinguibles.

Para ilustrar, reconsidérese la función cúbica del costo total de producción analizada en el cap 7. Supóngase que la verdadera función de costo total se describe de la siguiente manera, donde Y = costo total y X = producción.

-

Pruebas sobre variables omitidas y forma funcional correcta

En la práctica, nunca se está seguro de que el modelo adoptado para pruebas empíricas sea "el verdadero, total la verdad y nada más que la verdad". Con base en la teoría o en la introspección y en el trabajo empírico previo, se desarrolla un modelo, el cual se cree que recoge la esencia del tema en estudio. Luego, el modelo se somete a  una prueba empírica. Después de obtener los resultados, se inicia el "post mortem", teniendo en mente los criterios de un buen modelo estudiados anteriormente. Es en esta etapa cuando se viene a saber si el modelo seleccionado es adecuado. Al determinar la bondad de ajuste del modelo, se observan algunas características generales de los resultados, tales como el valor R², las razones t estimadas, los signos de los coeficientes estimados en relación con sus expectativas previas, el estadístico Durbin-Watson y similares. Si estos diagnósticos son razonablemente buenos, puede proclamarse que el modelo seleccionado es una buena representación de la realidad. Mediante el mismo procedimiento, si los resultados no aparecen estimulantes porque el valor de R² es muy bajo o porque muy pocos coeficientes son estadísticamente significativos o tienen los signos correctos o debido a que el d de Durbin-Watson es muy bajo, entonces puede empezar a preocupar la bondad del ajuste del modelo y se puede empezar a buscar remedios: Tal vez se ha omitido una variable importante, o se ha utilizado la forma funcional equivocada o no se ha realizado la primera diferenciación de la serie de tiempo (para eliminar la correlación serial) y así sucesivamente. Como una ayuda para determinar si la inadecuabilidad del modelo se debe a uno o más de estos problemas, se pueden utilizar al grupo algunos de los siguientes métodos.

Nivel de significancia nominal vs. nivel de significancia verdadero en presencia de dat-mining (II)

Por ejemplo, si c =15, k = 5 y α = 5%, utilizando (13.4.3), el verdadero valor de significancia es (15/5)(5) = 15%. Por consiguiente, si un investigador extrae datos y selecciona 5 de 15 regresores y solamente informa los resultados al nivel de significancia del 5% nominal y declara que estos resultados son estadísticamente significativos, esta conclusión se debe tomar con gran reserva.

Por supuesto, en la práctica los investigadores informan solamente los resultados finales, sin reconocer que llegaron a los resultados luego de una considerable data-mining. Posiblemente, una declaración en este sentido podría costarle al investigador la publicación de su trabajo y posiblemente un ascenso laboral y/o aun su posicion en la universidad!!

Nivel de significancia nominal vs. nivel de significancia verdadero en presencia de dat-mining (I)

Un peligro de la extracción de datos al cual se enfrenta el investigador desprevenido es que los niveles convencionales de significancia (α) tales como 1,5 o 10% no son verdaderos niveles de significancia. Lovell ha sugerido que si hay c candidatos regresores de los cuales k son finalmente seleccionados (k ≤ c) con base en el data-mining, entonces el verdadero nivel de significancia (α*) está relacionado con el nivel de significancia nominal (α) de la siguiente manera.

Detección de la presencia de variables innecesarias

Supóngase que se desarrolla un modelo de k variables para explicar un fenómeno:

Pruebas de errores de especificación

Conocer las consecuencias de los errores de especificación es una cosa pero averiguar si se han cometido tales errores es otra muy diferente, ya que en la especificación no es espera deliberadamente cometer estos errores. Muy frecuentemente, los sesgos de especificación surgen en forma inadvertida, posiblemente de nuestra incapacidad de formular el modelo en la forma más precisa posible debido a que la teoría subyacente es débil o a que no se tiene la clase de información adecuada para probar el modelo. La pregunta práctica no es cómo se cometen tales errores, pues generalmente los hay, sino cómo detectarlos. Una vez se encuentra que hay errores de especificación, con frecuencia, los remedios surgen por sí mismos. Si, por ejemplo puede demostrarse que una variable ha sido inapropiadamente omitida de un modelo, el remedio obvio es incluir esa variable en el análisis, suponiendo que se tiene información disponible sobre ésta. En esta sección se analizan algunas pruebas que pueden ser utilizadas para detectar errores de especificación.

Inclusión de una variable irrelevante (sobreespecificación de un modelo) (III)

La implicación de este hallazgo es que la inclusión de la variable innecesaria X3 hace que la varianza de α2 sea más grande de lo necesario, con lo cual se hace α2 menos preciso. Esto también es cierto de α1.

Obsérvese la asimetría en los dos tipos de sesgos de especificación que se han considerado. Si se excluye una variable relevante, los coeficientes de las variables consideradas en el modelo son generalmente sesgados al igual que inconsistentes, la varianza del error es incorrectamente estimada y los procedimientos usuales de prueba de hipótesis se invalidan. Por otra parte, la inclusión de una variable irrelevante en el modelo proporciona aun estimaciones insesgadas y consistentes de los coeficientes en el modelo verdadero, la varianza del error es correctamente estimada y los métodos convencionales de prueba de hipótesis son aún válidos; la única penalización que se paga por la inclusión de la variable superflua es que las varianzas estimadas de los coeficientes son mayores y como resultado, las inferencias probabílisticas sobre los parámetros son menos precisas. Una conclusión no deseada aquí sería que es mejor incluir variables irrelevantes que omitir variables relevantes. Pero esta filosofia no es estricta puesto que la adición de variables inneesarias conducirá a una pérdida de eficiencia de los estimadores y puede llevar también al problema de la multicolinealidad. Por queé? para no mencionar la pérdida de grados de libertad. Por consiguiente

En general, el mejor enfoque es incluir solamente las variables explicativas que, teóricamente, influyan directamente sobre la variable dependiente y no hayan sido tenidas en cuenta en otras variables incluidas.

Inclusión de una variable irrelevante (sobreespecificación de un modelo) (II)

De la fórmula MCO usual, se sabe que

Inclusión de una variable irrelevante (sobreespecificación de un modelo) (I)

Supóngase que

Omisión de una variable relevante (especificación insuficiente de un modelo) (VI)

Considérese ahora un caso especial en donde r23 = 0, es decir, X2 y X3 no están correlacionadas. En este caso, b32 será cero. Por qué? Por consiguiente, puede verse de (13.3.3) que α2 es ahora insesgada. También, de (13.3.4) y (13.3.5) parace ser que las varianzas de α2 y β2 son las mismas. No hay perjuicio entonces en eliminar la variable de X3 del modelo aun si ésta puede ser relevante teóricamente? La respuesta generalmente es no ya que en este caso la var(α2) estimada de (13.3.4) es aún sesgada y, por consiguiente, es probable que nuestros procedimientos de prueba de hipótesis continúen siendo dudosos. Además, en la mayoría de investigaciones económicas es probable que X2 y X3 estén correlacionadas, creando así los problemas mencionados anteriormente. El punto es muy claro: Una vez se ha formulado el modelo con base en la teoría relevante, no se aconseja eliminar una variable de dicho modelo.

Omisión de una variable relevante (especificación insuficiente de un modelo) (V)

Examínese ahora las varianzas de α2 y β2

Puesto que estas dos fórmulas no son las mismas, en general, la var(α2) será diferentede la var(β2). Pero se sabe que la var(β2) es insesgada (Por que?). Por consiguiente, la var(α2) está sesgada, lo cual reafirma la aseveración anterior. En el presente caso, la var(α2) parece más pequeña que la var(β2) siempre que r23 sea diferente de cero (es esto evidente?). Pero se debe tener cuidado aquí, ya que el σ² estimado a partir del modelo (13.3.2) y el estimado del verdadero modelo (13.3.1) no son los mismos porque la SRC de los dos modelos al igual que sus g de l son diferentes. Así, es muy posible que el error estándar de los estimadores del modelo mal especificado pueda ser más grande que aquél para el modelo correctamente especificado.

Omisión de una variable relevante (especificación insuficiente de un modelo) (IV)

Aunque las pruebas formales de las afirmaciones anteriores serían tema aparte, ya se han proporcionado algunas ideas sobre la naturaleza del problema en el apéndice 7A, sección 7A.5. Se mostró allí que (utilizando α2 en lugar de b12)

Omisión de una variable relevante (especificación insuficiente de un modelo) (III)

4. La varianza medida convencionalmente de

Omisión de una variable relevante (especificación insuficiente de un modelo) (II)

Las consecuencias de omitir X3 son las siguientes:

1. Si la variable excluida X3 está correlacionado con la variable incluida X2, es decir r23 es diferente de cero,  α1 y α2 son sesgados como también inconsistentes. Es decir, E(α1) no es igual a β1 y E(α2) no es igual a β2 e independientemente de qué tan grande sea la muestra, el sesgo no desaparece.
2. Aun cuando X2 y X3 no estén correlacionados (r23 = 0), α1 es aun sesgado, aunque α2 sea ahora insesgado.
3. La varianza de la perturbación σ² está incorrectamente estimada.

Omisión de una variable relevante (especificación insuficiente de un modelo) (I)

Supongase que el verdadero modelo es

Consecuencias de los errores de especificación

Independientemente de las fuentes de los errores de especificación, Cuáles son las consecuencias? Para mantener esta discusión simple, se responderá a esta pregunta en el contexto del modelo con tres variables y se considerarán en detalles dos tipos de errores de especificación, a saber, la omisión de una variable relevante y la adición de una variable superflua o innecesaria. Por supuesto los resultados se pueden generalizar al caso de k variables mediante manejo algebraico tedioso (una vez se tienen casos de más de tres variables, el álgebra matricial se convierte en necesidad.

Tipos de errores de especificación (V)

Para resumir, una vez se ha especificado un modelo como el modelo correcto, es probable que se comentan uno o más de los errores de especificación que a continuación se enumeran:

1. Omisión de una variable relevante, véase (13.2.2)
2. Inclusión de una variable innecesaria, véase (13.2.4)
3. Adopción de la forma funcional equivocada, véase (13.2.6)
4. Errores de medición, véase (13.2.7)

Antes de proceder, para empezar será conveniente saber la razón  por la cual se pueden cometer tales errores. En algunos casos, se sabe cuál es el modelo correcto pero no es posible implementarlo porque los datos necesarios no están disponibles. Así, en el análisis de la función de consumo, algunos autores han argumentado que además del ingreso, es peciso incluir la riqueza del consumidor como variable explicativa. Sin embargo, las cifras sobre riqueza son bastante difíciles de obtener y por esta razón, esa variable frecuentemente se excluye del análisis. Otra razón consiste en que se puede saber qué variables deben incluirse en el modelo pero quizás no se sabe la forma funcional exacta en la cual deben aparecer las variables en el modelo: Son frecuentes los casos en los cuales la teoría no indica la forma funcional precisa del modelo; tampoco dirá si el modelo es lineal en las variables o lineal en los logaritmos de las variables, o alguna mezcla de las dos posibilidades, o si tendrá alguna otra forma. Finalmente y quizás lo más importante, con frecuencia un error de especificación realmente es un error por una mala especificación del modelo puesto que, en primer término, no se sabe cuál es el verdadero modelo. Se tratará este punto mas adelante. 

Tipos de errores de especificación (IV)

En relación con el modelo verdadero, (13.2.6) también presenta un sesgo de especificación, siendo el sesgo en este caso orginado por el uso de una forma funcional incorrecta: En (13.2.1) Y aparece linealmente, mientras que en (13.2.6) ésta aparece en forma log-lineal.

Finalmente, considérese un investigador que utiliza el siguiente modelo:

Tipos de errores de especificación (III)

Si (13.2.1) es el "verdadero", (13.2.4) también constituye un error de especificación que consiste en incluir una variable innecesaria o irrelevante en el sentido de que el modelo verdadero supone que λ5 es cero. El nuevo término de error es, de hecho.

Tipos de errores de especificación (II)

Puesto que se supone que (13.2.1) es verdadero, la adopción de (13.2.2) constituiría un error de especificación, que consiste en la omisión de una variable relevante (Xi³). Por consiguiente, el término de error u2i en () es, de hecho

Tipos de errores de especificación (I)

Supóngase que con base en los criterios recién enumerados, se llega a un modelo que se ha aceptado como un buen modelo. Para ser concreto, este modelo sería.

Poder de predicción.

Para citar a Friedman nuevamente, "la única prueba relevante de la validez de una hipótesis [modelo] es la comparación de sus predicciones con la experiencia" Pero, no indica un valor elevado del R² el poder predictivo de un modelo? Sí, pero ese es su poder predictivo dentro de una muestra dada. Con lo que se desea contar es con su poder predictivo por fuera del periodo muestral. Como ejemplo, refiérase a la función de la demanda estimada de pollos en los Estados Unidos durante el período 1960-1982 dada en la ecuación (8.7.23), El valor del R² fue 0.9823, que es bastante alto. Pero, si se fuera a predecir la demanda de pollos más allá del período muestral (siempre que no se aleje mucho), se obtendría el mismo poder altamente explicativo?.

Consistencia teórica

Un modelo puede no ser bueno, a pesar de que se obtenga un R² elevado, si uno o más de los coeficientes estimados tienen los signos equivocados. En la función de demanda considerada en la ecuación (8.7.23), sí se obtuviera un signo positivo para el coeficiente del precio del pollo (una curva de demanda con pediente positiva) se deberían tener grandes sospechas sobre los resultados obtenidos.

Bondad del Ajuste

Puesto que la razón básica del diseño de modelos de regresión es explicar tanto como se pueda la variación de la variable dependiente a través de las variables explicativas incluidas en el modelo, se considera que un modelo es bueno si esta explicación, medida por el R², es tan alta como sea posible. Por supuesto, como se anotó anteriormente, no debe abusarse del criterio de un R² alto per se, sino más bien aceptar un R² alto siempre y cuando éste venga acompañado de otros criterios (por ejemplo, signos esperados a priori o valores esperados de los coefecientes).

Identificabilidad

Para un conjunto dado de datos, ésto significa que los parámetros estimados deben tener valores únicos o, su equivalente, que sólo debe haber un valor estimado para un parámetro dado. Para ver es concretamente, recuérdese el procedimiento de dos etapas de Durbin para resolver el problema de autocorrelación analizado en el capítulo anterior. En el primer paso se efectuó la siguiente expresión: